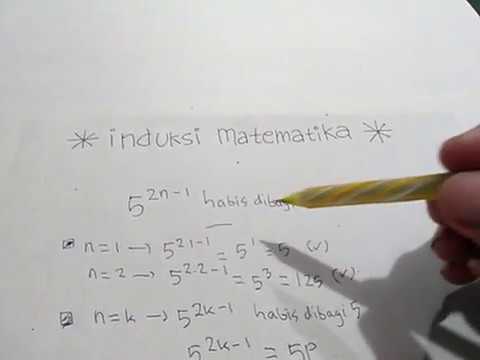Bilangan bulat a akan habis dibagi bilangan bulat b apabila dijumpai bilangan bulat m sehingga akan berlaku a bm. Contoh soal dan pembahasan habis di bagi dengan menggunakan induksi matematika ini ada dua.
Teori Bilangan
Contoh soal induksi matematika habis dibagi. Kita anggap 5 k 1 habis dibagi 4 untuk sebarang bilangan bulat. Induksi matematika materi yang membahas tentang pengertian materi pembahasan dan contoh soal induksi matematika secara lengkap dan terperinci. Contoh soal induksi matematika dan kunci jawaban bank soal induksi matematika dan kunci jawaban beserta pembahasan untuk siswa. Jadi berdasarkan induksi matematika konjektur kita tersebut benar. Jika kalian ingin memahaminya dengan jelas silahkan kalian simak materinya dibawah ini gaes. Apabila p habis dibagi a dan q habis dibagi a maka p q juga akan habis dibagi a.
Sebagai contoh 10 habis dibagi 5 benar karena terdapat bilangan bulat m 2 sehingga 10 52. Bilangan bulat a habis dibagi bilangan bulat b jika terdapat bilangan bulat m sehingga berlaku a bm. Berdasarkan dari prinsip induksi matematika tersebut terbukti bahwa 6 n 4 habis dibagi 5 untuk masing masing n bilangan asli. Misalnya 10 habis dibagi 5 benar sebab adanya bilangan bulat m 2 sehingga 10 52. Soal yang telah kami rangkum ini sering keluar dalam ulangan ataupun ujian nasional jadi insyaallah sangat bermanfaat untuk siswa pelajari. Misalnya 10 habis dibagi 5 benar sebab adanya bilangan bulat m 2 sehingga 10 52.
Berdasarkan prinsip induksi matematika yang telah dibahas terbukti jika 6 n 4 dapat habis dibagi 5 untuk tiap n bilangan asli tersebut. Semoga dengan contoh soal berikut bisa membantu pembelajaran matematika. Berdasarkan prinsip induksi matematika terbukti bahwa 6 n 4 habis dibagi 5 untuk setiap n bilangan asli. Bilangan bulat a akan habis dibagi bilangan bulat b apabila dijumpai bilangan bulat m sehingga akan berlaku a bm. Misalnya 10 habis dibagi 5 benar karena terdapat suatu bilangan bulat m 2 sehingga 10 52. Bilangan bulat a habis dibagi bilangan bulat b jika terdapat bilangan bulat m sehingga berlaku a bm.
Untuk saat ini akan dibahas pembuktian suatu persamaan yang habis dibagi dengan menggunakan induksi matematika. Gunakan induksi matematika untuk menunjukkan bahwa 5 n 1 habis dibagi 4 untuk semua bilangan bulat positif n. Induksi matematika merupakan materi yang menjadi perluasan dari logika matematikalogika matematika sendiri mempelajari pernyataan yang bisa bernilai benar atau salah ekivalen atau ingkaran sebuah pernyataan dan juga berisi penarikan kesimpulan. Berdasarkan dari prinsip induksi matematika tersebut terbukti bahwa 6 n 4 habis dibagi 5 untuk masing masing n bilangan asli. Untuk n 1 yang sangat jelas habis dibagi 4.
Gallery of Contoh Soal Induksi Matematika Habis Dibagi
